JW Spelling Bee 2: Why Not Include "S"?

Why Not Include "S"?

Why indeed did the NYT editors decide to omit "S" from Spelling Bee puzzles? Did they look at any data? Or did they just go by instinct? 

They might have considered a basic high-school math counting principle tells us that including S increases the possible combinations of 7 letters from 480,700 (25 choose 7) to 657,800 (26 choose 7) -- an increase of 37%. But how many of those combinations are valid puzzlecombos (i.e., 7 letter combinations that yield a pangram)? 

I used Mathematica to dig into the problem and determine the actual effects of including S in Spelling Bee. As it turns out, the number of puzzlecombos jumps from 4802 (with no S) to 9482, an increase of 97%. So adding S to the mix has an outsized effect on increasing the number of available puzzlecombos. This makes intuitive sense when you consider how many words contain S.

Effect of S on the Spelling Bee puzzle universe

I asked Mathematica to solve all 66,374 puzzles (i.e., 7 x 9482) that are possible when including S. (I set it to work before I went to bed, and while I slept, it solved all those puzzles!) The histogram below shows the results. As I expected, the shape of the histogram is the same as the one with S omitted, but it's scaled up: the bars are higher, the tail is longer (one of the puzzles has 630 possible words!). 

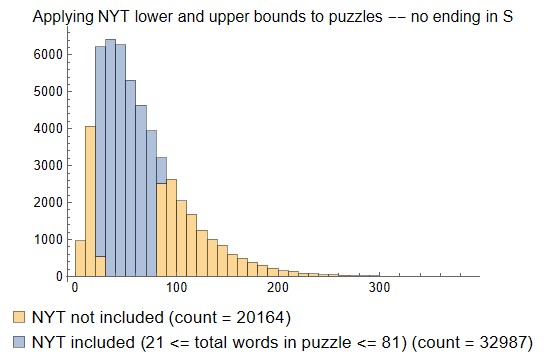
A reminder from my previous blog that NYT has not (to date) published any puzzles with fewer than 21 words or more than 81 words. If we apply these two bounds to the data above, we get the histogram below. 

Applying these bounds causes more than half of the possible puzzles to be omitted! The upper bound, in particular, takes a big bite out out the available puzzles (29,727 to be exact, vs. only 4179 for the lower bound). 

Below is the same histogram for puzzles that do NOT include S. The blue bars -- which represent the "within bounds" puzzles -- total 20,819. The corresponding blue bars above total 32,468. Including S yields 56% more possible puzzles even after applying the upper and lower bounds. So the NYT could introduce more variety into the puzzles by including S and just enforcing their lower and upper bounds. 

One guess at how the NYT arrived at their current situation is this: First, they decided to omit S from the puzzles, thinking "this will take care of the 'too many words in a puzzle' problem." Then someone discovered that even with omitting S, some puzzles still fell into the "too many words" trap. So they started enforcing a de facto upper bound. It was too late for them at that point to just say, "let's include S and just take care of the 'too many words' issue through an upper bound." 

But all those damn plurals

An alternative narrative to the one I pose above is that removing S from the game is worthwhile because puzzle doers will find the process of adding S to so many words just plain tedious. "Plurals are boring, so let's get rid of them." Okay, maybe there's a point to be made there. So what if we replaced the rule "No words contain S" with "No words end with S"? How would that affect things?

As it turns out, when you apply the rule "no words end with S," the resulting data is remarkably similar to the data for "no words containing S." In both cases, 38% of the puzzles are "within NYT bounds." Compare the graph below with the one immediately above. They look almost identical except for the scale of the vertical axis. The big advantage of the rule "no words end with S" over the current "no words contain S" is that it yields 58% more possibilities for valid puzzles. 

Hey, NYT Puzzle Editors! 

Here's my recommendation to the NYT puzzle editors: Change your rule "no words containing S" to "no words ending in S." Doing so would open the game up to a greater variety of puzzles (welcome to the game, S!), and would maintain the same sweet spot of "interesting without being too challenging or tedious" that they've built a reputation for. 

Back to unicorns and other extremes

In my previous blog, I introduced the notion of a unicorn -- i.e., puzzles with only 1 solution (the pangram). Adding S to the mix actually gives us 3 more unicorns! So here they are -- all the pangrams from unicorn puzzles:

• amphibian
• foxhound
• jukebox
• pharynx
• sixfold
• smallpox
• snuffbox
• viburnum

I think it's cool that there are only 9 words in the English language that have this property. 

And what about the opposite of a unicorn? That would be this particular puzzle: adeirst (the underscored letter is the middle letter). It has a whopping 630 solution words. Some day if the NYT is feeling really cheeky, they might publish this one . . . maybe just for an hour on April Fools Day to drive the famous Steve G from Sound Beach, NY into fits. (Steve G publishes hints for all solution words every day in the comments section of Spelling Bee.)

The "stingiest" puzzlecombo is bejkoux, which has only 28 solution words in all 7 of its puzzles. At the other extreme is aeiprst, which has 3544 solution words in all 7 of its puzzles and features all of the following pangrams:

asperities, aspirate, aspirates, parasite, parasites, parities, parties, pastier, pastries, patisserie, patisseries, piaster, piasters, pirates, raspiest, repatriates, separatist, separatists, striptease, stripteaser, stripteasers, stripteases, tapestries, traipse, traipses

I hope my explorations have been interesting. I welcome your feedback and ideas for future exploration!